Chemistry 30

Answer the following questions based on the potential energy diagram shown here:

1. Does the graph represent an endothermic or exothermic reaction?
2. Label the postion of the reactants, products, and activated complex.
3. Determine the heat of reaction, ΔH, (enthalpy change) for this reaction.
4. Determine the activation energy, E_a for this reaction.
5. How much energy is released or absorbed during the reaction?
6. How much energy is required for this reaction to occur?

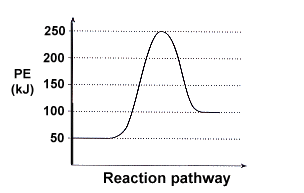Solution

1. The graph represents an endothermic reaction
2. the reactants, products, and activated complex are shown

c. ΔH = +50 kJ.

Since this in an endothermic reaction, ΔH will have a positive value. ΔH is the difference in energy between the energy levels of the initial reactants (50 kJ) and the final products (100 kJ), and does not depend on the actual pathway (remember Hess's Law?)

d. E_a = +200 kJ.

Activation energy is the amount of energy required to go from the energy level of the reactants (50 kJ) to the highest energy point on the graph, the activated complex (250 kJ).

e. 50 kJ of energy are absorbed during this endothermic reaction

(this is the value of ΔH)

f. 200 kJ of energy are required for this reaction to occur ( E_a).

Even though ΔH is only 50 kJ, enough energy must be supplied to reach the activated complex, or the reaction will not occur.

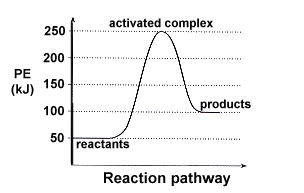Sketch a potential energy curve that is represented by the following values of ΔH and E_a. You may make up appropriate values for the y-axis (potential energy).

ΔH = -100 kJ and E_a = 20 kJ

Is this an endothermic or exothermic reaction?

Solution:

Since ΔH is a negative number, we know that the reaction is exothermic. Therefore, begin by sketching an exothermic potential energy graph:

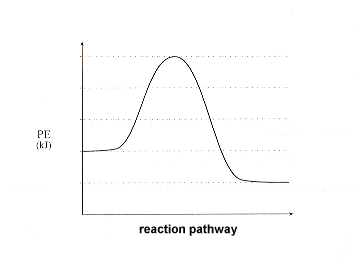Next, assign values to the y-axis that will satisfy our requirements, namely

ΔH = -20 kJ and E_a = +60kJ

Remember:

• ΔH is the difference between energy levels of the reactants and products - this difference will equal -20 kJ.
• E_a is the difference between energy levels of the initial reactants and the peak of the curve, the activated complex.

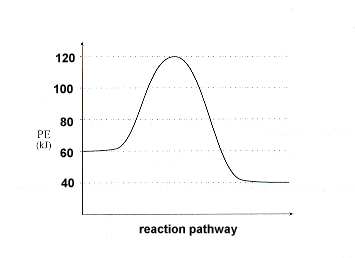In the next unit we will be discussing reactions that are reversible, and can go in either the forward or reverse directions. For example, hydrogen gas and oxygen gas react to form water, but water can also be broken down into hydrogen and oxygen gas. We typically write a reaction that can be reversed this way, using the double arrow symbol ( or ↔):

2 H₂ + O₂ ↔ 2 H₂O

This reaction is exothermic in the forward direction:

2 H₂ + O₂ ↔ 2 H₂O + 285 kJ

but endothermic in the reverse direction:

2 H₂O + 285 kJ ↔ 2 H₂ + O₂

Consider a general reversible reaction such as:

A + B ↔ C + D

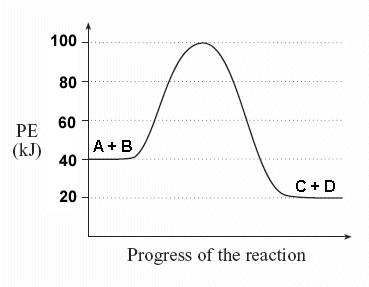Solution:

You should immediately see that the forward reaction is exothermic - the products (C + D) are at a lower energy level than the reactants.

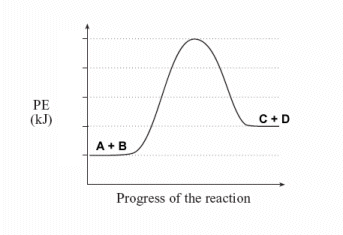
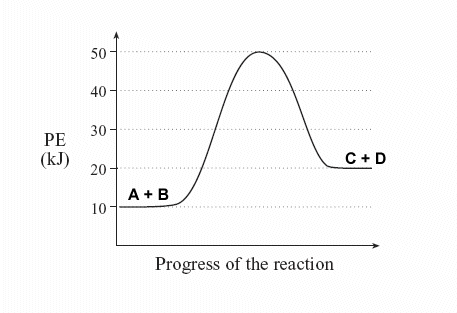
Sketch a potential energy diagram for a general reaction A + B ↔ C + D

Given that ΔH_reverse = -10 kJ and E_{a forward} = +40 kJ

Solution:

• Begin by determining whether the forward reaction (A + B → C + D) is endothermic or exothermic:
  
  
• Since ΔH_reverse = -10 kJ you can determine that ΔH_forward = +10 kJ (same value, just change the sign).
  
  Since ΔH_forward is positive you know that the forward direction of the reaction is endothermic. Begin by sketching a general endothermic potential energy curve that is endothermic. Don't worry about drawing to scale at this time:

• At what energy level should you put the activated complex, the top of the peak? Since E_{a forward} = +40 kJ, you know that from the initial reactants (A + B) you need to go up 40 energy units. Pick any value for a starting energy level (let's use a starting point of 10 here), then add 40 to find the peak of your graph.
  
  
• Return to ΔH to determine the energy level of the products. Since ΔH_forward = +10 kJ, add 10 to our starting value to determine the energy level of the products: