Chemistry 30

There is another way to calculate the heat of reaction, using bond enthalpies. Bond enthalpy refers to the amount of energy stored in the chemical bonds between any two atoms in a molecule. Bond enthalpies have been experimentally determined and can be found in a Table of Bond Enthalpies.

Important Data Table Bond Enthalpies Pick a format: Word | RTF | PDF

The net change in energy during a chemical reaction is the difference between how much energy it takes to break chemical bonds and how much energy is released when bonds form. So if we know how much energy is stored in these chemical bonds, we can calculate the change in energy for a reaction. The energy change will equal:

To solve bond enthalpy questions, you'll need to be able to draw the structural formulas of models, something you likely learned in Chemistry 20. You'll need to know which atoms are bonded together, and if single, double, or triple bonds are involved. We'll keep our molecules pretty simple here.

Let's look at a few examples.

Example 1. Using bond enthalpies, provided in the table below, calculate the heat of reaction, ΔH, for:

Given the following bond enthalpies:

Solution:

Draw structural formulas for all molecules. Pretty simple for these molecules:

Chemical formula	Structural Formula
H2	H — H
Cl2	Cl — Cl
HCl	H — Cl

Using the balancing coefficients in the balanced equation and the structural formulas, determine how much energy is required to break all of the bonds of the reactants, and how much energy is released when all of the product bonds form:

	REACTANTS: BOND BREAKING						PRODUCTS: BOND FORMATION
Bond	No. bonds per molecule		Bond Enthalpy		Total Energy		No. bonds per molecule		Bond Enthalpy		Total Energy
H - H	1	×	436	=	436
Cl - Cl	1	×	243	=	243
H-Cl							1	×	433	=	433

We still need to use the balancing coefficients from the balanced equation:

For example, 1 mole of H - H bonds requires 436 kJ but in our balanced equation only ½ mole of H - H bonds is involved, which will require only 218 kJ (436 × 0.5):

Example 2: Using the bond enthalpies provided, calculate the heat of reaction, ΔH, for:

C₂H₄(g) + H₂(g) → C₂H₆(g)

Given the following table of bond enthalpies:

C — H	413 kJ
C = C	614 kJ
C —C	348 kJ
H — H	436 kJ

Solution: Begin by drawing the structural formulas for all molecules.

Chemical formula	Structural Formula
C2H4
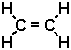C2H6
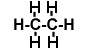H2	H — H

Determine how many bonds of each type are present in each molecule, and calculate the bond energies. For example, in C₂H₄ there is a single C=C bond (a double bond) but there are four C - H bonds.

	REACTANTS: BOND BREAKING						PRODUCTS: BOND FORMATION
Bond	bond enthalpy		Number bonds per molecule		Total Energy		bond enthalpy		Number bonds per molecule		Energy
C - H	413	×	4	=	1652		413	×	6		2478
C = C	614	×	1	=	614
H - H	436	×	1	=	436
C - C							348	×	1	=	348

Finally calculate ΔH for the reaction, being sure to check for coefficients from the balanced equation:

C2H4(g) + H2(g) → C2H6(g) ΔH = Σ(reactant bonds) – Σ(product bonds) ΔH = (1652 + 614 + 436) – (2478 + 347) ΔH = 2702 – 2826 = -124 kJ   answer

Complete the assignment.